ydsolve – additional math algorithms

Functions

ydsolve.interp(ys, xs, x)

Linear interpolation/extrapolation between specified points.

Extrapolation is based on 2 closest to x points.

Prerequisites:

  • Lists ys and xs must be the same size;

  • Lists ys and xs must contain at least 2 points;

  • List xs must contain ascending or descending values (list is not checked to save performance).

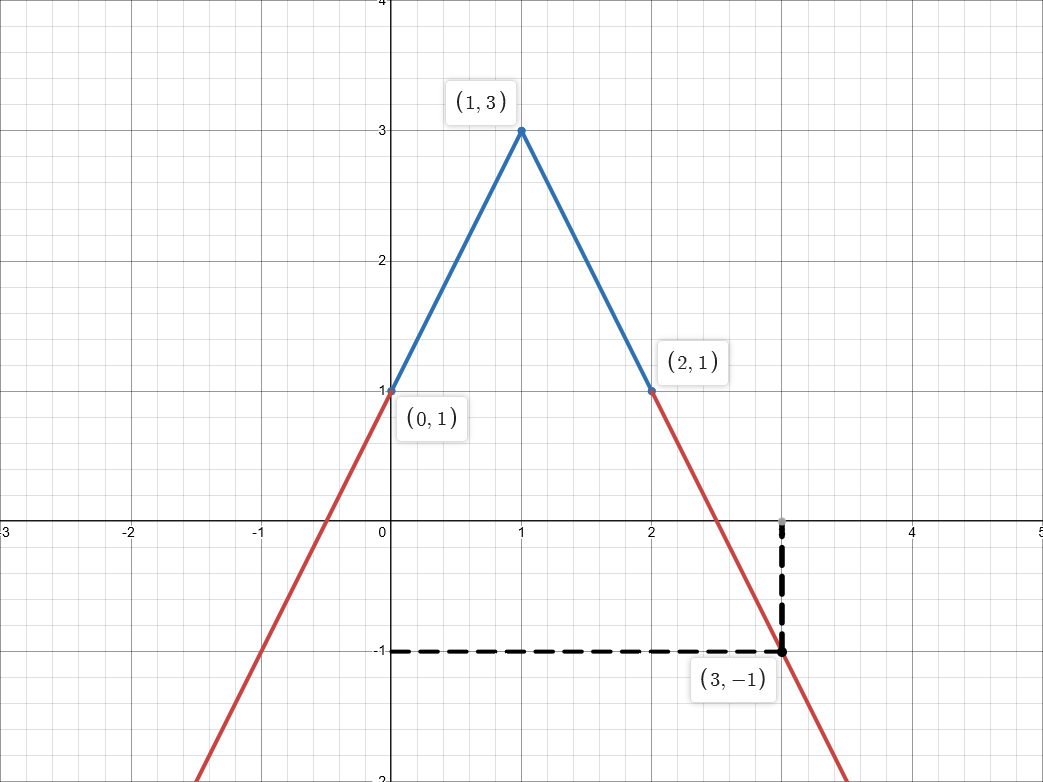
Usage example
from ydsolve import interp

# sample points (x, y)
Xs = [0, 1, 2]
Ys = [1, 3, 1]

x = 3
y = interp(Ys, Xs, x)
print(y) # -1
_images/ydsolve_example_interp.png
Parameters:
ydsolve.calcpoly(ys, xs, rows=3)

Calculates polynomial coefficients using list of predefined points (x, y).

You need at least rows number of sample points to calculate polynomial coefficients.

Parameters:
Returns:

Polynomial coefficients (offset, x, x^2, …)

Return type:

tuple[float]

ydsolve.evalpoly(coeffs, x)

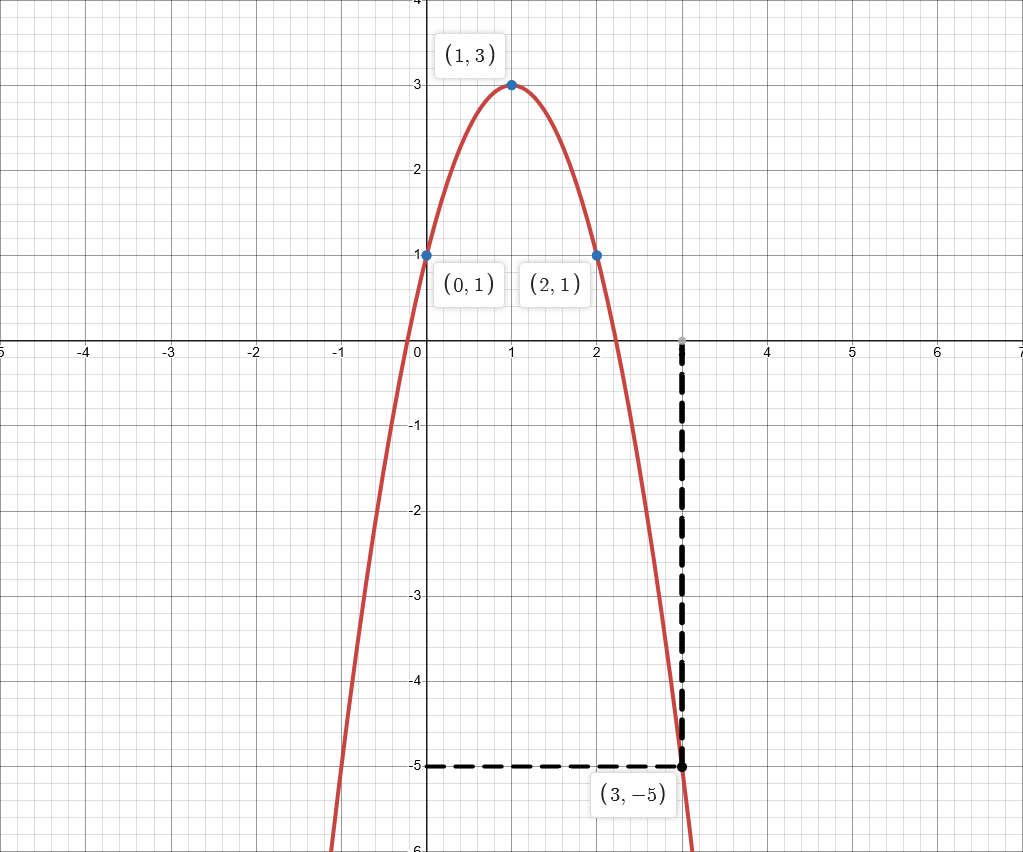
Evaluates polinomial at x.

Usage example
from ydsolve import calcpoly, evalpoly

# sample points (x, y)
Xs = [0, 1, 2]
Ys = [1, 3, 1]

poly = calcpoly(Ys, Xs, 3) # calculate polynomial coefficients
print(poly) # (1.000001, 3.999993, -1.999996) floating point precision limitation

# evaluation
x = 3
y = evalpoly(poly, x)
print(y) # -4.99999
y = poly[0] + poly[1]*x + poly[2]*x*x
print(y) # -4.99999, the same calculation as evalpoly()
_images/ydsolve_example_evalpoly.png
Parameters:
Return type:

float

Classes

class ydsolve.LeastSqr(rows=3)

Solves a linear system using the method of least squares. Can be useful for calibrating external sensors.

The number of parameters in the linear system is defined by rows. Supported range: [2..16]. Performance will be noticeably reduced if more than 5 parameters are used.

Usage example
import ydsolve

# Sample points
Ys = (3, 5.1, 9.8, 13.3)
Xs = (1, 2, 3, 4)

# Class example
ls = ydsolve.LeastSqr(rows=3)
ls.addpoly(Ys[0], Xs[0])
ls.addpoly(Ys[1], Xs[1])
ls.addpoly(Ys[2], Xs[2])
ls.addpoly(Ys[3], Xs[3])
coeffs = ls.solve()
print(coeffs) # (0.6500188, 1.809981, 0.3500038)

# Polynomial usage
x = 2.5
y = coeffs[0] + coeffs[1]*x + coeffs[2]*x*x
print(y) # 7.362495

# Method example
coeffs2 = ydsolve.calcpoly(Ys, Xs, 3)
print(coeffs == coeffs2) # True

Methods

init(rows=3)

Reinitialize the solver using the specified number of parameters.

Parameters:

rows (int) – Number of parameters. Range: [2..16].

deinit()

Frees occupied memory. init() must be called to reuse deinitizlied object.

reset()

The solver will be reset to its initial state, removing all added samples. The number of parameters will remain unchanged.

count()
Returns:

Number of samples added.

Return type:

int

add(y, x1, x2[, x3[, x4[, x5[, ...]]]])

Add a sample row to the calculation. The number of parameters is defined by the rows in the class constructor.

addpoly(y, x)

Used to calculate polynomial coefficients from predefined points.

Equivalent to: add(y, 1.0, x, x*x, x*x*x, x*x*x*x, ...)

solve()

Solves a linear system. The number of coefficients returned is determined by the rows in the class constructor.

Returns:

Calculated coefficients of linear system.

Return type:

tuple[float]